ediriyanto: November 2011

Konsep Fungsi Trigonometri

Turunan fungsi aljabar telah kalian kuasai, bagaimana dengan turunan fungsi trigonometri?
mari kita pahami rumusnya serta berlatih di soal dan pembahasan turunan fungsi trigonometri bersama-sama, dijamin sukses dalam ujian kalian….

Untuk menentukan turunan trigonometri sama dengan konsep awal mencari turunan, namun disini langsung kita ambil hasilnya….
dimana $f' (x) = \underset{h\rightarrow 0}{lim}\:\frac{f(x + h) - f(x)}{h}$ maka
Turunan pada fungsi trigonometri akan mempunyai rumus :

$f(x) = sin\:x$ maka $f'(x)= cos\:x$

$f(x) = cos\:x$ maka $f'(x)= - sin\:x$

$f(x) = a.sin\:(bx+c)$ maka $f'(x)= ab.cos\:(bx+c)$

$f(x) = a.cos\:(bx+c)$ maka $f'(x)= -ab.sin\:(bx+c)$

contoh:
$1.\:f(x)= 3cos\:x$ maka $f'(x)=-3sin\:x$
$2.\:f(x)=2sin\:5x$ maka $f'(x)=10cos\:5x$
$3.\:f(x)=4.cos(3x+\pi)$

$\begin{array}{rcl}f'(x) & = & {-4}.3.sin(3x+\pi)\\ & = & {-12}.sin(3x+\pi)\end{array}$

Rumus rumus yang dipakai di turunan fungsi aljabar, berlaku pula untuk mengerjakan turunan fungsi trigonometri maupun gabungan keduanya lets try this….

$1.\:f(x)=sec\:x$ tentukan f ‘(x) ! jawab

$\begin{array}{rcl}f(x) & = & sec\:x\\ & = & \frac{1}{cos\:x}\end{array}$

$\begin{array}{lcl}u=1 & maka & u'=0\\ v=cos\:x & maka & v'=-sin\:x\end{array}$

$\begin{align*}f'(x) & = & \frac{u'.v-v'.u}{v^2}\\ & = & \frac{0.cos\:x-(-sin\:x).1}{(cos\:x)^2}\\ & = & \frac{sin\:x}{cos^2\:x}\\ & = & \frac{sin\:x}{cos\:x}.\frac{1}{cos\:x}\\ & = & tan\:x.sec\:x\end{align*}$

$2.\:f(x)=(x^2+2).sin\:x$ tentukan f ‘(x)! jawab:

$\begin{array}{lcl}u=x^2+2& maka & u'=2x\\v=sin\:x & maka & v'=cos\:x\end{array}$

$\begin{array}{rcl}f'(x) & = & u'.v+v'.u\\ & = & 2x.sin\:x+cos\:x.(x^2+2)\\ & = & 2x\:sin\:x+x^2.cos\:x+2\:cos\:x\end{array}$

Turunan ke-n
diberikan fungsi f(x), maka turunan pertama dari f(x) adalah f ‘(x) ; turunan kedua dari f(x) adalah f ”(x) ; turunan ketiga dari f(x) adalah f ”’(x) dst.
$1.\:f(x)=4x^2.cos\:x$ tentukan turunan kedua dari f(x)! jawab.

*kita cari turunan pertama dulu ya..

$\begin{array}{lcl}u=4x^2 & maka & u'=8x\\ v=cos\:x & maka & v'=-sin\:x\end{array}$

$\begin{array}{rcl}f'(x) & = & u'.v+v'.u\\ & = & 8x.cos\:x+(-sin\:x).4x^2\\ & = & 8x.cos\:x-4x^2.sin\:x\end{array}$

*perhatikan untuk $f'(x)=8x.cos\:x-4x^2.sin\:x$ mempunyai dua suku kita misalkan bahwa suku-suku f ‘(x) adalah a dan b dimana f ‘(x) = a – b untuk mencari turunan kedua akan berlaku f ”(x) = a’ – b’ mari kita cari turunan masing-masing suku…

*ambil suku pertama dari f ‘(x) kita misalkan 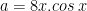$a=8x.cos\:x$

$\begin{array}{lcl}u=8x & maka & u'=8\\ v=cos\:x & maka & v'=-sin\:x\end{array}$

$\begin{array}{rcl}a' & = & u'.v+v'.u\\ & = & 8.cos\:x+(-sin\:x).8x\\ & = & 8.cos\:x-8x.sin\:x\end{array}$

*ambil suku kedua dari f ‘(x) kita misalkan 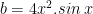$b=4x^2.sin\:x$

$\begin{array}{lcl}u=4x^2 & maka & u'=8x\\ v=sin\:x & maka & v'=cos\:x\end{array}$

$\begin{array}{rcl}b' & = & u'.v+v'.u\\ & = & 8x.sin\:x+(cos\:x).4x^2\\ & = & 8x.sin\:x+4x^2.cos\:x\end{array}$

kembali ke $f''(x)=a'-b'$

$\begin{array}{rcl}f ''(x) & = & a'-b'\\ & = & (8.cos\:x-8x.sin\:x)-(8x.sin\:x+4x^2.cos\:x)\\ & = & 8.cos\:x-8x.sin\:x-8x.sin\:x-4x^2.cos\:x\\ & = & 8.cos\:x-16sin\:x-4x^2.cos\:x\end{array}$

$2.\:f(x)=x.cos\:x+sin\:x$ tentukan turunan ke-empat dari f(x) ! jawab:

$*f(x)=x.cos\:x+sin\:x$ mempunyai dua suku kita misalkan a dan b sehingga f ‘(x) = a ‘ + b ‘ cari turunan masing-masing suku dulu ya…

$a=x.cos\:x$

$\begin{array}{lcl}u=x & maka & u'=1\\ v=cos\:x & maka & v'=-sin\:x\end{array}$

$\begin{array}{rcl}a' & = & u'.v+v'.u\\ & = & 1.cos\:x+(-sin\:x).x\\ & = & cos\:x-x.sin\:x\end{array}$

$b=sin\:x$ maka $b'=cos\:x$

$\begin{array}{rcl}f'(x) & = & a'+b'\\ & = & (cos\:x-x.sin\:x)+(cos\:x)\\ & = & 2.cos\:x-x.sin\:x\end{array}$

$*f'(x)=2.cos\:x-x.sin\:x$ mempunyai dua suku kita misalkan lagi c dan d sehingga f ”(x) = c ‘ – d ‘

$c=2.cos\:x$ maka $c'=-2.sin\:x$

$d=x.sin\:x$

$\begin{array}{lcl}u=x & maka & u'=1\\ v=sin\:x & maka & v'=cos\:x\end{array}$

$\begin{array}{rcl}d' & = & u'.v+v'.u\\ & = & 1.sin\:x+cos\:x.x\\ & = & sin\:x+x.cos\:x\end{array}$

$\begin{array}{rcl}f''(x)& = & c'-d'\\ & = & (-2.sin\:x)-(sin\:x+x.cos\:x)\\ & = & {-2}.sin\:x-sin\:x-x.cos\:x\\ & = & {-3}.sin\:x-x.cos\:x\end{array}$

$*f''(x)=-3.sin\:x-x.cos\:x$ mempunyai dua suku, suku pertama langsung dapat kita turunkan dan turunan suku kedua dapat dilihat telah kita cari di atas $a=x.cos\:x$ maka $a'=cos\:x-x.sin\:x$

sehingga

$\begin{array}{rcl}f'''(x) & = & {-3}.cos\:x-(cos\:x-x.sin\:x)\\ & = & {-3}.cos\:x-cos\:x+x.sin\:x\\ & = & {-4}.cos\:x+x.sin\:x\end{array}$

$*f'''(x)={-4}.cos\:x+x.sin\:x$ mempunyai dua suku, suku pertama langsung dapat kita turunkan dan turunan suku kedua dapat dilihat telah kita cari di atas $d=x.sin\:x$ maka $d'=sin\:x+x.cos\:x$

sehingga

$\begin{array}{rcl}f''''(x) & = & {-4}.(-sin\:x)+(sin\:x+x.cos\:x)\\ & = & {4}.sin\:x+sin\:x+x.cos\:x\\ & = & {5}.sin\:x+x.cos\:x\end{array}$

begitu seterusnya hingga turunan ke-n …..

3. Jika diketahui $y=sin\:x$ buktikan bahwa turunan ke-n yaitu $y^n=sin(x+\frac{\pi}{2}.n)$ !
jawab:

*ingatlah kembali nilai sin x di tiap kuadran

$y=sin\:x$

$y'=cos\:x$	$=\:sin(\frac{\pi}{2}+x)$	$=\:sin(x+\frac{\pi}{2}.1)$
$y''=-sin\:x$	$=\:sin({\pi}+x)$	$=\:sin(x+\frac{\pi}{2}.2)$
$y'''=-cos\:x$	$=\:sin(\frac{3.\pi}{2}+x)$	$=\:sin(x+\frac{\pi}{2}.3)$
$y''''=sin\:x$	$=\:sin({2.\pi}+x)$	$=\:sin(x+\frac{\pi}{2}.4)$
… … dst	… … dst	… … dst
sehingga	$y^n=\:sin(x+\frac{\pi}{2}.n)$

ediriyanto

Senin, 28 November 2011

F.Konsep Fungsi Trigonometri

Konsep Fungsi Trigonometri