ediriyanto: 2011

Jumat, 16 Desember 2011

Relasi

1. Pengertian Relasi
Sebelum mempelajari Relasi, kalian harus menguasai materi prasyaratnya yaitu : himpunan, anggota himpunan, dan himpunan bagian dari suatu himpunan.

Contoh :
Pak Teguh mempunyai tiga orang anak, yaitu Doni, Pipit, Dimas. Masing-masing
anak mempunyai kegemaran berolahraga yang berbeda-beda.

Doni gemar berolah raga voly dan renang.
Pipit gemar berolah raga voly,
Dimas gemar berolah raga basket dan sepak bola.

Sedangkan Doni dan Pipit mempunyai kegemaran berolah raga yang sama yaitu voly. Jika anak-anak Pak Teguh dikelompokkan menjadi satu dalam himpunan A, maka anggota dari himpunan A adalah Doni, Pipit, Dimas.

Himpunan A tersebut kita tuliskan sebagai
A = {Doni, Pipit, Dimas}.

Sedangkan jenis olah raga yang digemari anak-anak Pak Teguh dapat dikelompokan dalam himpunan B.

Himpunan B dituliskan
B = {Voly, Renang, Basket, Sepak bola}

Terhadap kegemaran anak-anak pak Teguh terdapat hubungan antara himpunan A dan himpunan B. Hubungan tersebut berkait dengan gemar berolah raga dari anak-anak pak Teguh yang di sebut “relasi”

Relasi dari himpunan A ke himpunan B adalah
aturan yang memasangkan anggota-anggota himpunan A dengan anggota-anggota himpunan B

Cara Menyatakan Suatu Relasi
Suatu relasi dapat dinyatakan dengan tiga cara, yaitu dengan diagram panah, diagram Cartesius, dan himpunan pasangan berurutan

Misalkan:
P = {Dini, Arif, Alyn, Rizky},
Q = {Matematika, IPS, Kesenian, IPA, bahasa Inggris},
dan “pelajaran yang disukai”adalah relasi yang menghubungkan himpunan P ke himpunan Q

Dengan Diagram Panah

P	Q

Dengan Diagram Cartesius

Dengan Himpunan Pasangan BerurutanRelasi "pelajaran yang disukai" yang menghubungkan himpunan P ke himpunan Q dapat dinyatakan dengan himpunan pasangan berurutan sebagai berikut :

{(Dini, Matematika); (Dini, IPA); (Arif, Matematika); (Arif, Inggris);
(Alyn, Matematika); (Alyn, IPA); (Alyn, Inggris); (Rizky, IPS); (Rizky, Seni)}

sumber :http://www2.jogjabelajar.org/web2009/smp-mtk/03_relasi-dan-fungsi/f_home.htm

B.Konsep Fungsi Kuadrat

Konsep Fungsi Kuadrat

Fungsi dari Garis lengkung yang menarik untuk dipelajari adalah fungsi yang mempunyai bentuk persamaan kuadrat. Di alam ini yang secara tidak langsung lengkungan yang mempunyai bentuk persamaan kuadrat telah anda kenal adalah bentuk-bentuk pada jembatan gantung, daun jendela yang lengkung, jarak yang ditempuh oleh lemparan

bola secara vertical terhadap waktu Gambar 6.3.1
Lintasan Bola berupa Parabola (Gambar 6.3.1) dan masih banyak lagi contoh contoh fungsi kuadrat.

Grafik fungsi kuadrat ini disebut Parabola. Parabola diperoleh dengan menentukan tempat kedudukan atau
himpunan semua titik-titik yang berjarak sama terhadap sebuah garis l dan sebuah titik (Gambar 6.3.2).Titik tetap tersebut dikatakan focus dan garis tersebut dikatakan Garis arah. Jika fokus F disebelah atas titik asal, misalkan di ),0( p , garis arah kita ambil di sebelah bawah titik asal dengan persamaan py -= , dan jika suatu titik ),( yx terletak pada lengkungan parabola jika dan hanya jika

Persamaan (6.3.1) disebut Bentuk Baku sebuah Persamaan parabola yang terbuka ke atas, dan jika p > 0 maka p merupakan jarak dari fokus ke puncaknya. Fungsi kuadrat mempunyai 2 jenis baku yang berbentuk Parabola, tergantung dari terbukanya parabola mengarah kemana. Misalkan 2 persamaan parabola diberikan oleh pyx 4= , jika p > 0 maka parabola terbuka keatas dan jika p < 0 maka terbuka kebawah. Kedua jenis parabola itu dapat dilihat pada Gambar 6.3.3.

sumber :http://outsiders17.blogspot.com/2009/12/konsep-persamaan-fungsi-kuadrat.html

D.Konsep Fungsi Eksponen

Konsep Fungsi Eksponen

Fungsi eksponen merupakan pemetaan bilangan real x ke a^xdengan a > 0 dan

Jika a > 0 dan

maka

disebut fungsi eksponen

mempunyai sifat-sifat :

(i) Kurva terletak di atas sumbu x (definit positif)

(ii) Mempunyai asimtot datar y = 0 (sumbu x )

(iii) Monoton naik untuk a > 1

(iv) Monoton turun untuk 0 <>

Grafik fungsi eksponen y = a^x

(i) y = a^x : a > 1

(i) y = a^x 0 <>

Contoh:
Buatlah grafik dari y = 2^x!
Jawab: Buatlah tabel yang menunjukkan hubungan antara x dan y = f (x) = 2^x . Dalam hal ini pilih nilai x sehingga y mudah ditentukan.

3. Persamaan fungsi Eksponen
Ada beberapa bentuk persamaan eksponen, diantaranya adalah:

- F ( x ) = 1

- Untuk f(x)

0 dan f(x)

1, maka f(x) = g(x)

- f ( x ) = -1 asalkan f (x) dan g (x) sama-sama genap atau sama-sama ganjil,

- f ( x ) = 0 asalkan f ( x ) > 0 dan g ( x ) > 0

Contoh :
Tentukan nilai x supaya

Jawab:

4. Pertidaksamaan Eksponen

1. f ( x ) > g ( x ), 0 > 1

2. f ( x ) <>

Contoh:

Himpunan bilangan real yang memenuhi pertidaksamaan

adalah....
Jawab:

Jadi HP = { x | x > 2 }

sumber :http://hernakuncoro.blogspot.com/2010/02/eksponen.html

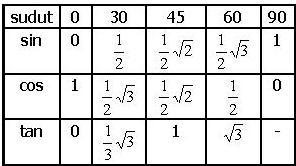
Menghafalkan Sudut-sudut Istimewa dengan Tangan

Pada tulisan sebelumnya saya telah menguraikan tentang bagaimana mengingat konsep trigonometri pada segitiga siku-siku. Nah, berikut ini, kita akan mempelajari bagaimana menghafalkan sudut-sudut istimewa pada kuadran I (0, 30, 45, 60 dan 90) dengan menggunakan konsep kaidah TANGAN KIRI, perhatikan gambar berikut :

: tangan kiri untuk membantu menghafal sudut istimewa

Cara menggunakannya,

perhatikan nilai pada pergelangan tangan (itu patokannya) —-> 1/2 akar (n)

dan perhatikan nilai sudut untuk x = 0, 30, 45, 60 dan 90 yang ditulis pada kuku, dimulai dari kuku jari kelingking (x=0) diibaratkan nol nilai yg kecil makanya ditulis di kelingking dan seterusnya hingga (x=90) ditulis pada kuku ibujari yg diibaratkan nilai paling besar.

Nilai n yang dipakai untuk sin x (berwarna hijau) dimulai n = 4 pada ibujari terus hingga n = 0 pada kelingking, jadi penggunaanya, sbb :

n= 4 —-> sin 90 = 1/2.akar(4) = 1/2.(2) = 1

n= 3 —-> sin 60 = 1/2.akar(3)

n = 2 —->sin 45 = 1/2.akar(2)

n = 1—-> sin 30 = 1/2.akar(1) =1/2

n = 0 —->sin 0 = 1/2.akar(0) = 0

Nilai n yang dipakai untuk cos x (berwarna merah) dimulai n = 0 pada ibujari hingga n = 4 pada kelingking, untuk penggunaanya bisa anda cobakan sendiri

sehingga nantinya kita bisa menyimpulkan sebagai berikut :

INGAT : untuk mendapatkan nilai tangen (tan) cukup kita bagi nilai sin dengan cos karena kita tau bahwa ,
tan x = sin x/ cos x
Nah, begitulah cara menghafalkan sudut istimewa pada trigonometri, SEMOGA BISA MEMBANTU !!!

Sumber : http://muhar5yah.wordpress.com/2008/10/25/menghafalkan-sudut-sudut-istimewa-dengan-tangan/

Trigonometri

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segi tiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.
Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri. Lagadha adalah matematikawan yang dikenal sampai sekarang yang menggunakan geometri dan trigonometri untuk penghitungan astronomi dalam bukunya Vedanga, Jyotisha, yang sebagian besar hasil kerjanya hancur oleh penjajah India.
Matematikawan Yunani Hipparchus sekitar 150 SM menyusun tabel trigonometri untuk menyelesaikan segi tiga.
Matematikawan Yunani lainnya, Ptolemy sekitar tahun 100 mengembangkan penghitungan trigonometri lebih lanjut.
Matematikawan Silesia Bartholemaeus Pitiskus menerbitkan sebuah karya yang berpengaruh tentang trigonometri pada 1595 dan memperkenalkan kata ini ke dalam bahasa Inggris dan Perancis.

Trigonometri sekarang ini

Ada banyak aplikasi trigonometri. Terutama adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.
Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanik, teknik sipil, grafik komputer, kartografi, kristalografi.
Ada pengembangan modern trigonometri yang melibatkan "penyebaran" dan "quadrance", bukan sudut dan panjang. Pendekatan baru ini disebut trigonometri rasional dan merupakan hasil kerja dari Dr. Norman Wildberger dari Universitas New South Wales. Informasi lebih lanjut bisa dilihat di situs webnya [1].

sumber :http://id.wikipedia.org/wiki/Trigonometri

Koordinat Cartesius dan Polar

Koordinat Kartesius dan Koordinat Kutub

Cara lain dalam menyajikan letak sebuah titik pada bidang xy selain koordinat kartesius adalah dengan koordinat kutub

Pada gambar 2.11 titik P(x,y) pada koordinat kartesius dapat disajikan dalam koordinat kutub dengan P(r, α) seperti pada gambar 2.12. Jika koordinat kutub titik P(r, α) diketahui, koordinat kartesius dapat dicari hubungan:
$cos\alpha =\frac{x}{r}n \to x=rcos\alpha$
$sin\alpha =\frac{y}{r}n \to y=rsin\alpha$ jika koordinat kartesius titik P(x,y) diketahui, koordinat kutub titik P(r, α) dapat dicari dengan hubungan:
$r=\sqrt{x^{2}+y^{2}}$
$tan\alpha =\frac{y}{x}n \to \alpha =arctan\frac{y}{x}$ ,arc tan adalah invers dari tan

from :http://sastrawati21.blogspot.com/2011/01/trigonometri.html

D.Luas Segitiga

Pembuktian Luas Segitiga = 1/2a.b.sinC

Pernahkah kamu melihat rumus luas segitiga seperti di bawah?

Rumus Luas segitiga ini sering dipakai, namun, kadang banyak orang tidak mengetahui bagaimana penurunannya.. Langsung saja kita lihat bagaimana contoh penggunaannya.
Contoh Soal:

Segitiga ABC dengan panjang a=5 cm, dan b =6 cm. Sudut di titik C adalah 20⁰. Maka, tentukan luas segitiga tersebut!
Jawab:

(menggunakan kalkulator)Note: a, b, dan c sesungguhnya hanya masalah simbol. Yang esensi dari rumus ini yaitu kita bisa mencari luas segitiga jika diketahui:
*) 2 sisi segitiga, dan
*) sebuah sudut yang diapit kedua sisi tersebut.
=========================================================================

Bukti Rumus

Penurunannya sangat mudah.. Lihat segitiga di bawah.